AVATARES GRÁFICOS

JUGANDO CON LAS LÍNEAS CURVAS

CON LÍNEAS ONDULADAS, ESPIRALES, BUCLES Y PARÁBOLAS

CON LA CIRCUNFERENCIA

EL ÓVALO

Es una curva cerrada y plana compuesta por un número par de arcos de circunferencia enlazados entre sí y simétricos respecto sus ejes mayor y menor normales entre sí.

Construir un óvalo conociendo el eje mayor

Dado el eje mayor AB, lo dividimos en tres partes iguales. Por sus divisiones trazamos dos circunferencias O1 y O2 de radio la tercera parte del eje AB, estas se cortan en los puntos O3 y O4.

O1, O2, O3 y O4 son los centros de los cuatro arcos que compondrán el óvalo. Los arcos de centro O1 y O2 tienen como radio la tercera parte del eje mayor y son tangentes a las trazadas con centro en O3 y O4, los puntos de enlace T2, T4, T1 y T3 de las circunferencias O1 Y O2 con O3 y O4 respectivamente están donde los segmentos unión de centros correspondientes corten a las circunferencias de centros O1 y O2. El radio de los arcos de centro O3 y O4 será por tanto la distancia existente entre ellos y sus correspondientes puntos de enlace (O3-T2).

ESPIRALES

La espiral es una curva abierta y plana generada por el movimiento de un punto que se aleja de otro u otros fijos denominados centros. Puede estar constituida por arcos de circunferencia enlazados entre sí y de radios gradualmente mayores. Se denomina espira al fragmento de curva que describe el punto en una vuelta completa.

Las espiras contiguas distan entre sí una magnitud constante denominada paso.

Construimos una espiral de dos centros conocido el paso.

Dados los dos centros A y B, se unen entre sí y se prolonga el segmento que determinan, esta recta será inicio y fin de los sucesivos arcos que determinan la espiral. La magnitud del paso es igual al doble de la magnitud del segmento AB.

Para trazarla, hacemos centro en A o B y describimos una semicircunferencia de radio AB que corta en C a la recta, cambiamos de centro (a B en la ilustración) y trazamos otra semicircunferencia con el mismo sentido y a continuación de la anterior, a partir de C, de radio BC y por tanto igual a P obteniendo en su intersección sobre la recta el punto D desde donde trazamos otra con centro en A y radio 3P/2 y así sucesivamente. Observaremos que el radio de las semicircunferencias aumenta P/2 en cada ocasión.

LA LÍNEA CURVA

La línea curva 

es una línea continua que varía de dirección paulatinamente.

• Curvas cerradas son por ejemplo la circunferencia y la elipse.
• Curvas abiertas son por ejemplo la parábola y la espiral.

Circunferencia: es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.

Elipse: es la curva simétrica cerrada y plana que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría.

Parábola: es una curva abierta resultante de una porción circular o eliptica.

Espiral: es una línea curva abierta generada por un punto que se va alejando progresivamente del centro a la vez que gira alrededor de él.

¿Quién es JOAN MIRÓ?

HISTORIA DEL CUADRO "INTERIOR HOLANDÉS"

ENLACES DE INTERÉS:

• Fundación Miró - http://www.bcn.fjmiro.es
• Museo Reina Sofía - http://www.museoreinasofia.es/coleccion/FichaObras.php?idautor=16
• Página con obras pictóricas - http://www.allposters.es/gallery.asp?
• Juego interactivo - http://www.museothyssen.org/pequenothyssen/default.html
• Juego interactivo - http://www.brooklynkids.org/patternwizardry/games.html
• Página para colorear y jugar – http://caxigalines.mareasdepoesia.net
• Página para pintar y colorear – http://usuarios.lycos.es/miniclub/colorea/colorea.htm

DIBUJANDO HOJAS Y PLANTAS

CLASIFICACIÓN DE LAS HOJAS SEGÚN SU FORMA

CLASIFICACIÓN DE LAS HOJAS SEGÚN SU BORDE

LÁMINA 2.1. Dibujamos una hoja del Arce blanco también llamado "Falso Plátano" a partir de un eje de simetría. Técnica con ceras blandas: rayado y fundido.

1. Colorea con ceras blandas fundiendo los colores. Utiliza colores ocres, naranja y amarillo.

2. Copia la otra mitad de las hoja siguiendo las líneas de simetría.

LÁMINA 2.2.  Recorto y pego hojas a partir de distintas forma de plegado del papel. Utilizamos hojas de revistas o papel charol.

• Eje de simetría vertical. Debe salir la hoja y su silueta.
• Doblado en acordeón y unidas
• Doblado en acordeón separadas.

LÁMINA 2.3. Divide tu lámina en cuatro cuadrantes con dos perpendiculares centradas.

Dibuja cuatro tipos de hoja a partir de su eje de simetría.
Consulta la página principal y elige entre los tipos de hojas y sus bordes.

LÁMINA 2.4. Copia el modelo que tienes en el libro de conocimiento del medio.

Materiales: 

Regla, compás, lápiz de grafito, papel de revista, tijeras, pegamento, rotuladores y ceras blandas.

HOJAS Y FRUTOS DE ALGUNOS ÁRBOLES

LOS MEJORES LIBROS DEL ARTE BOTÁNICO... enlaza

LA ILUSTRACIÓN BOTÁNICA: CIENCIA Y ARTE... Enlaza

TRAZAMOS LÍNEAS PERPENDICULARES

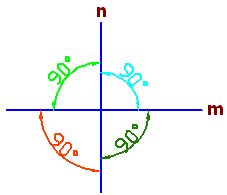
Rectas perpendiculares son las que al cortarse forman cuatro ángulos iguales de 90º

Las rectas m y n son perpendiculares porque al cortarse forman 4 ángulos de 90º.

1. PERPENDICULAR EN EL CENTRO DE UN SEGMENTO

En la figura siguiente tenemos el segmento 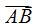 y con un radio un poco mayor que la mitad del segmento y haciendo centro en A trazamos dos arcos como los tienes dibujados a continuación:

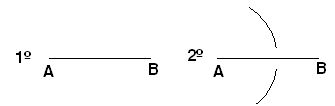
Con el mismo radio y haciendo centro en B trazas otros dos arcos que se cortan en C y D quedándote:

Ahora unes los puntos de intersección de los arcos, puntos C yD, con una recta y ésta, será perpendicular al segmento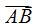 

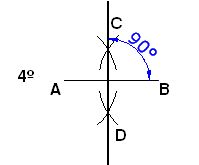
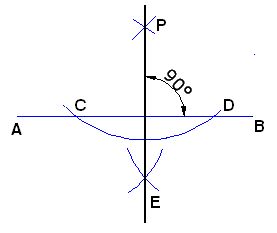
2. PERPENDICULAR A UN SEGMENTO DESDE UN PUNTO DADO:

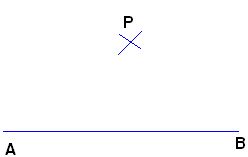
Como ves, se trata de trazar una perpendicular al segmento 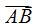 desde el punto P.

Tomas el compás y con un radio capaz de cortar al segmento 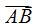en dos puntos  C y D trazas el arco correspondiente:

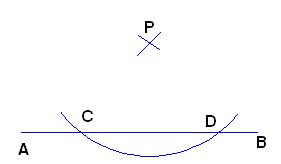
Volvemos a hacer uso del compás, hacemos centro en C y D con un radio algo mayor de la mitad del segmento 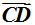y trazamos los dos arcos que tienes a continuación cuyo punto de intersección es el punto E:

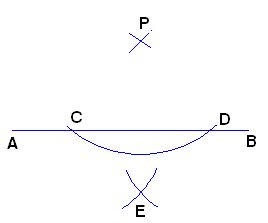
Ahora sólo nos falta unir los puntos E y P. La recta que une ambos puntos es perpendicular a :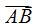

3. PERPENDICULAR A UN SEGMENTO POR UNO DE SUS EXTREMOS:

En primer dibujamos el segmento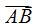 

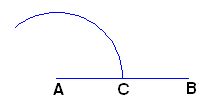
Con un compás y haciendo centro en A, que será el punto de intersección con la perpendicular que trazaremos después, con un radio cualquiera (este radio lo usarás varias veces) trazamos un arco:

Ahora, con centro en C, y con el mismo radio trazamos otro arco:

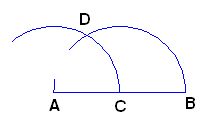
Los arcos que hemos dibujado se han cortado en D.

Con el mismo radio, y con centro en D, trazamos el arco siguiente:

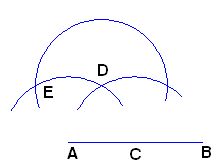
Con el mismo radio y centro en E dibujamos el arco que ves en la figura siguiente:

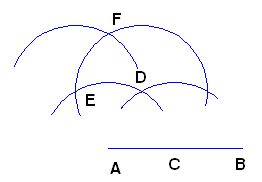
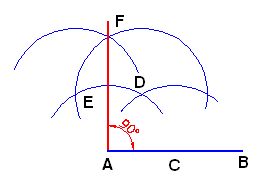
Por último, no tienes más que unir los puntos A y F para obtener la perpendicular al segmento 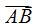 en el origen A: